Звук. Часть 4

Сейчас предстоит познакомиться с еще одной характеристикой, еще одним и, кстати говоря, исключительно важным понятием. Имя ему — спектр.

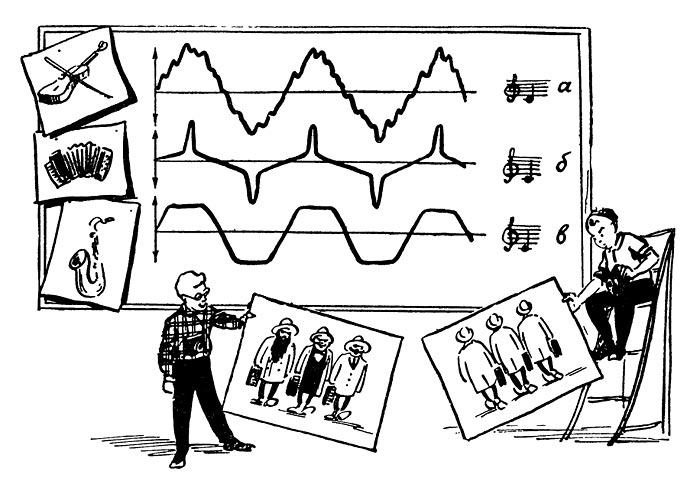
Рис. 5. Одинаковые по высоте (частоте) звуки, исполненные на различных музыкальных инструментах, звучат по-разному. Характер звучания определяется формой кривой (спектром).

Для начала поясним, почему мы назвали спектр «исключительно важным» понятием. Представьте себе, что несколько музыкантов, например, пианист, скрипач, баянист и трубач, взяли на своих инструментах одну и ту же ноту. Забегая немного вперед, скажем, что при этом все четыре инструмента создают звуковые волны с одним и тем же периодом. Можно рассадить музыкантов так, что в определенной точке все четыре звуковые волны будут создавать и одинаковое давление. Но никаким способом не удастся добиться, чтобы звуки, идущие от разных инструментов, были неотличимо похожи друг на друга. Вы прекрасно знаете, что скрипка и труба всегда звучат по-разному даже тогда, когда берут одну и ту же ноту.

Чем же отличаются, казалось бы, одинаковые звуки, исходящие из разных инструментов? Они отличаются пока еще загадочным для нас спектром.

Очень часто учебная модель какого-либо прибора или аппарата устроена намного проще оригинала. Делают это для того, чтобы сразу не запугивать ученика и сложность реальной техники раскрывать перед ним постепенно. Исходя из подобных побуждений, и мы выбрали для первого знакомства чрезвычайно упрощенный образец звуковых колебаний (рис. 1 и 4). В основном, было сделано два упрощения, два отклонения от истины, и, пожалуй, сейчас можно честно рассказать о каждом из них.

На рис. 5 приведено несколько графиков реальных звуков. Во многом все они похожи: имеют одинаковый период колебаний, одинаковую амплитуду. В то же время сразу видно, что все эти звуки сильно отличаются один от другого и от «учебного» (рис. 1 и 4). Они отличаются формой кривой. А за этими, казалось бы, сухими словами «форма кривой» скрывается очень многое — весь ход изменения звукового давления. Вы видите, что в одном случае (рис. 5, а) звуковое давление изменяется очень неуверенно — в течение каждого полупериода оно несколько раз становится то больше, то меньше. Второй график (рис. 5, б) показывает, что сжатие и разрежение существует лишь небольшую часть периода, а все остальное время звуковое давление близко к нулю. Совсем иначе проходят колебания в третьем случае (рис. 5, в). Здесь звуковое давление почти весь период действует с наибольшей амплитудной силой.

Кроме уже знакомой струны, существует огромное множество источников звука, которые создают самые разнообразные звуковые колебания с самой причудливой формой кривой. Наше ухо, а мы его назвали главным потребителем звуковых волн, довольно точно различает все эти звуки. Иными словами, ухо каким-то образом оценивает не только силу, не только частоту звука, но и форму кривой его графика.

Из всего сказанного придется сделать невеселый вывод. Путешествуя по зоопарку, мы не заметили слона; изучая звуковые колебания, не ввели очень важный для них параметр — форму кривой. Но как только захотим исправить эту ошибку, то сразу же столкнемся с серьезными, на первый взгляд даже непреодолимыми трудностями. Как можно точно оценить форму графика? В каких единицах ее измерять? Как сравнивать разные по форме кривые, отмечать их сходство или различие?

Для начала попробуем решить подобную задачу из другой области. Представьте себе, что вам нужно, пользуясь картой, измерить площадь какого-либо водоема, например Черного моря. В этом случае можно поступить так: разбить всю поверхность моря на квадраты, посчитать площадь каждого из них, а затем все полученные результаты сложить. При этом на карте разместятся два-три больших квадрата, несколько

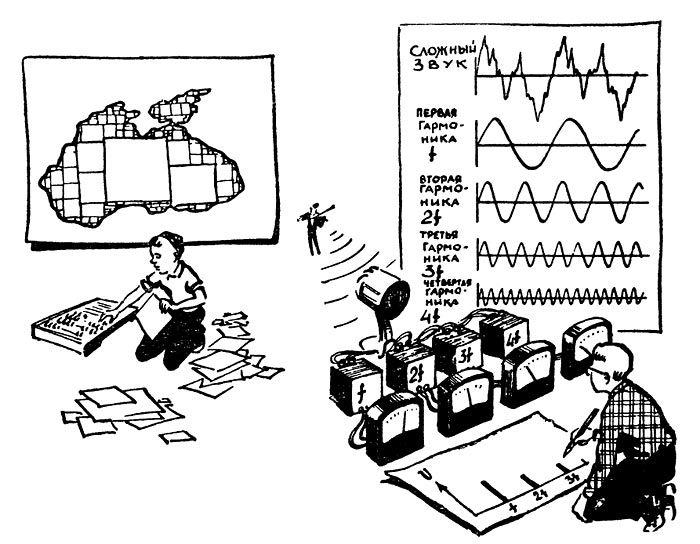
Рас. 6. Звук сложной формы можно представить в виде суммы простейших синусоидальных составляющих (гармоник) с разными частотами и амплитудами. Такой набор синусоидальных составляющих называется спектром сложного звука.

квадратов поменьше и, наконец, множество мелких и мельчайших квадратиков, которые точно воспроизведут сложные очертания морских берегов (рис. 6).

Подобным же образом для оценки формы кривой какого-либо звука его можно представить как сумму каких-то составляющих— звуков с разными амплитудами, частотами и фазами, но с одинаковой стандартной формой кривой. В этом случае сравнительно просто описать форму графика любого, самого сложного звука. Нужно лишь назвать набор стандартных составляющих, которые в сумме дадут этот сложный звук.

То, что сложную геометрическую фигуру можно представить в виде суммы более простых фигур, в частности квадратов, ясно и без особых рассуждений. А вот можно ли подобную операцию суммирования производить со звуковыми колебаниями? Оказывается, можно.

Если в точку, где расположен измеритель звукового давления, направить две звуковые волны, то прибор не будет в отдельности реагировать на каждую из них, а покажет суммарное давление. Это как раз и означает, что для получения звуковых колебаний сложной формы достаточно сложить, то есть заставить совместно работать, определенный набор простых по форме звуков. И наоборот, всякий сложный звук можно разложить на более простые составляющие.

Пока слово «можно» мы применили условно, имея в виду «в принципе можно». Однако в дальнейшем вы познакомитесь с приборами, которые без всяких условностей, в буквальном смысле слова могут разложить сложный звук на набор простых составляющих. Кстати, один из таких приборов — это наше ухо.

Из чего же нужно исходить при выборе стандартной составляющей для разложения сложных звуков?

Какому из многочисленных простых графиков здесь следует отдать предпочтение?

Решать эти вопросы нам уже не придется — составляющая, наиболее удобная для разложения сложных колебаний, в том числе и сложных звуков, уже выбрана.

Выбор пал на простейшую кривую, известную под названием «синусоида». Примером синусоидальных (иногда говорят, гармонических) колебаний может служить «учебный» звук, а его график (рис. 4), так же как и график колебаний «учебной» струны и маятника (рис. 1 и 3), представляет собой типичную синусоиду. Чем же привлекла к себе внимание эта кривая?

Прежде всего нужно сказать, что синусоиду выбрала сама природа. Природа создала прибор — ухо животных и человека, которое может выделять из сложного звука простейшие составляющие, причем именно синусоидальные. Синусоида — очень популярная кривая. Графики бесчисленного множества различных колебаний — электрических, механических, световых, молекулярных, химических — имеют вид синусоиды или, во всяком случае, очень ее напоминают. Ну, и в заключение отметим, что, по-видимому, нужно было сказать в самом начале. Синусоида обладает рядом замечательных математических свойств, благодаря которым природа «считает» самым естественным, самым удобным, самым простым видом колебаний именно синусоидальные.

Итак, будем считать, что выбор сделан. Теперь, чтобы описать форму кривой сложного звука, достаточно указать эквивалентный ему набор синусоидальных колебаний, который называется спектром сложного звука. Спектр принято изображать в виде особого графика, напоминающего частокол (рис. 6). Из этого графика сразу же видно, каковы частоты отдельных составляющих и какую амплитуду имеет каждая из них.

В начале XIX века французский математик Жан Батист Жозеф Фурье предложил формулы, по которым можно вычис-лись амплитуды всех синусоидальных составляющих сложного звука. Одновременно было доказано: если рисунок на графике сложного звука периодически повторяется, то в спектре наверняка будут гармоники — синусоидальные (гармонические) составляющие с частотами, кратными основной частоте, то есть частоте сложного звука. Так, например, если основная частота /= 100 гц, то в спектре будут составляющие с частотами 100 гц (первая гармоника, частота /), 200 гц (вторая гармоника, частота 2/), 300 гц (третья гармоника, частота 3/) и т. д. Как правило, чем выше номер гармоники, тем меньше ее амплитуда. Математическое описание спектра, составленного из гармоник, носит название «ряд Фурье».

Потом мы в основном будем иметь дело с периодическими звуками, спектр которых состоит только из гармоник. Если же в спектр, кроме гармоник, придется вводить еще какую-нибудь составляющую, то мы будем считать, что это «ЧП» — чрезвычайное происшествие, и сразу же обратим на него внимание.

Научившись с помощью спектра — набора гармоник — точно описывать форму сложной кривой, мы в какой-то мере исправили первое упрощение, сделанное при знакомстве с «учебной» струной. Струна не создает синусоидальные колебания, как это показано на рис. 1, и спектр колебаний реальной струны содержит целый ряд гармоник (рис. 6).

Знакомясь с колебаниями струны, мы сделали еще одно упрощение, и его также следует исправить. Для этого достаточно сильней натянуть «учебную» струну, чтобы в несколько раз повысить частоту ее колебаний. Без этого колебания воздуха, которые создает струна, вообще нельзя будет считать звуком. Почему?

Как видно из графиков, период колебаний в нашем примере составляет 0,1 сек, а значит, частота равна 10 гц. В то же время ухо воспринимает акустические колебания с частотами от 16 гц до 22 кгц. Слышимым звуком можно называть только те колебания, которые укладываются в этот диапазон. Неслышимые акустические колебания с частотой ниже 16 гц называют инфразвуком, а выше 22 кгц — ультразвуком.

Более подробно об этом будет рассказано в следующем разделе, который в основном посвящен замечательному творению живой природы — органу слуха.

Когда вы отвечаете на телефонный звонок или просто обращаетесь к собеседнику, то не задумываетесь о том, что стойт за простым выражением: «Я вас слушаю». За этими словами скрывается очень многое: тончайшие и во многом загадочные химические реакции, работа сложных, до сих пор не понятых инженерами физических приборов и вычислительных машин, о которых современная кибернетика пока только мечтает. Еще стоят за этими словами поражения и победы, борьба за право жить на Земле, полная драматизма бурная история, которая рассказывает о событиях, происходивших сотни миллионов лет назад.

Геологическая химия установила, что возраст Земли составляет примерно 5,3 миллиарда лет и что жизнь зародилась на нашей планете около миллиарда лет назад.

Миллиард лет — это очень большой срок. За это время можно было бы 300 миллионов раз пешком обойти вокруг земного шара или 15 миллионов раз «сходить» на Луну и обратно. За это же время обычным стаканом можно 200 раз вычерпать всю воду из Азовского моря. А если каждый день сбрасывать у своего дома хотя бы несколько десятков лопат земли, то через миллиард лет по соседству с вами появится гора, значительно более высокая, чем Эльбрус. Вот что такое миллиард лет.

И все же этот срок не кажется очень большим, когда вспоминаешь, как много он должен был вместить событий, связанных с развитием живой природы.

Сейчас на Земле найдено и описано более 500 тысяч видов растений и 1100 тысяч видов животных и насекомых, в том числе 50 тысяч видов позвоночных животных. Все это изумительное многообразие берет свое начало от простейших одноклеточных организмов, а может быть, даже от какого-нибудь одного типа самых примитивных живых клеток. Неутомимый мастер — природа усложняла простейшие клетки, создавала клеточные коллективы-организмы, прилаживала их к условиям окружающей среды, отбраковывала слабые и плохо приспособленные образцы. Природа закрепляла наиболее важные, полезные свойства и способности, повышала квалификацию отдельных клеток и формировала из клеток-специалистов органы особого назначения, такие, как плавник или крыло, глаз или сердце. Из поколения в поколение совершенствовался мир живого, управляемый железными законами изменчивости, наследственности и естественного отбора. В результате титанической, ни на секунду не прекращавшейся работы природа за миллиард лет создала такие шедевры, как организм человека, состоящий из 20 триллионов невидимых химических комбинатов — четко взаимодействующих живых клеток.

Растения развивались в сравнительно спокойной обстановке. Они прямо на месте получали все необходимое для жизни: от солнечных лучей — энергию, из почвы — строительный материал, разнообразные минеральные вещества, из дождевого облака — влагу. И поэтому, как ни совершенствовались растения, приспосабливаясь к морям и пустыням, зною и холоду, они так навсегда и остались неподвижными.

Другое дело животные. Они должны были сами искать для себя пищу и при этом еще не стать пищей какого-нибудь более сильного «коллеги». Вот почему в животном мире, начиная с его простейших представителей, выживало и развивалось то, что могло хорошо двигаться и ориентироваться. Вот почему у животных до такой высокой степени развились органы движения и нервная система.

Нервная система — это сложный орган, а точнее, целый комплекс взаимосвязанных органов, с помощью которого организм изучает окружающий мир, непрерывно оценивает обстановку и на основе этого организует свое поведение. Развитие нервной системы и особенно ее главного штаба — головного мозга — в итоге оказалось решающим фактором в борьбе за существование, за прогресс того или иного вида животных.

Сбор информации об окружающем мире организм осуществляет с помощью рецепторов. Это специализированные клетки (Иван Петрович Павлов называл их клетками-осведо-мителями), которые под действием света, тепла, давления или химических веществ посылают определенные сигналы в нервную систему. Некоторые рецепторы появились на довольно ранних стадиях развития живого организма. Так, в частности, приемники света, фоторецепторы, разбросаны по всему телу дождевого червя, представителя древнейшего типа животных— кишечнополостных. Некоторое подобие фоторецепторов встречается даже у одноклеточных. У сложных животных ре-цепторные клетки объединяются в целые органы, такие, как глаз (знаете ли вы, что глаз человека содержит около 200 миллионов светочувствительных клеток?), органы обоняния и вкуса.

Рецепторы звуковых колебаний, а значит, и орган слуха появились намного позже других, так как острая необходимость в них возникла сравнительно недавно, «всего» 150—200 миллионов лет назад. К этому времени наиболее смелые представители подводного мира (а жизнь, как известно, зародилась и развивалась в океане), стали выбираться на берег, постепенно превращаясь в сухопутных животных. В земных условиях звуковые волны приносят исключительно важные «сообщения» — журчание ручья, шаги приближающегося хищника, шорохи убегающей «пищи». Необходимость пользоваться этой информацией и привела к появлению и развитию слуха.

Слуховой аппарат развился из так называемой боковой линии рыб — своеобразного органа давления, точнее, цепочки органов, вытянувшихся от головы до хвоста по обеим сторонам рыбьего тела. Боковая линия реагирует на медленные изменения давления, позволяет рыбам огибать препятствия, чувствовать приближение других рыб и даже «слышать» некоторые звуки. В частности, установлено, что рыба голец слышит звуки с частотой до 3 кгц, гольян — до 7 кгц и сомик — до 12,4 кгц. В последнее время проведено много интересных опытов, в которых рыб приучали реагировать на различные звуки: например, двигаться за пищей, ориентируясь на источник звуковых волн.

Но услышать звук — это еще далеко не все, нужно проанализировать его, отличить одни звуки от других. Таким анализом занимается мозг, и именно от его развития в огромной степени зависит совершенство всего слухового аппарата. Так у рыб наблюдаются простейшие реакции на звук — обычно они просто бегут от источника звуковых колебаний. Животные амфибии уже умеют выделять некоторые особо важные для них звуковые комплексы, еще лучше развит слух у птиц, и, наконец, у млекопитающих, к классу которых относимся и мы с вами, слуховой аппарат достигает высочайшей степени совершенства, становится одним из главных средств сбора информации об окружающем мире.